![\includegraphics[]{mersenne.eps}](../../../downloads/mersenne/singlefile/img3.png)
Marin Mersenne
![\includegraphics[]{mersenne.eps}](../../../downloads/mersenne/singlefile/img3.png)
Denne opgave skal handle om Mersenne primtal, men kommer også ind på meget andet. Da de forskellige grene af matematikken ofte vikler sig ind i hinanden på en uforudsigelig måde, må vi have fat i ting som f.eks. gruppeteori, for at kunne forstå argumenterne i forbindelse med beviset af Lucas-Lehmer sætningen.
Jeg skrive i et tekstformateringssystem som hedder LATEX. Denne rapport ser derfor ikke helt ud, som hvis den var lavet med f.eks. Word. Henvisninger til litteraturlisten bagerst står i teksten som f.eks “[1]”, hvilket skal læses som “kilde 1”.
I forhold til Word har mine sider en større margin, både i siderne og i top og bund. Det betyder naturligvis, at der ikke står så meget på hver linie, og at der ikke er så mange linier på hver side. Opsætningen er valgt sådan, fordi det er nemmere at læse en tekst, når linierne ikke er alt for lange.
Én side i LATEX indeholder omkring 70% af hvad der kan stå på en side i Word, når vi snakker om ren tekst. Når det også er ligninger med på siden bliver forholdet endnu større, idet LATEX bruger mere luft omkring ligningerne end Word vil gøre.
Tager man disse ting i betragtning, mener jeg, at opgaven har den rigtige størrelse.
Vi vil starte med at se generelt på primtal. Mersenne primtal er blot primtal som opfylder nogle yderligere krav, men derfor stadig også opfylder de generelle krav til primtal.
Forskellige tal har forskellige divisorer. Ethvert helt tal ![]() har de
såkaldte trivielle divisorer
har de
såkaldte trivielle divisorer ![]() ,
, ![]() ,
, ![]() og
og ![]() . Andre
divisorer kaldes ægte divisorer ifølge [13, s.
168].
. Andre
divisorer kaldes ægte divisorer ifølge [13, s.
168].
Nogle tal har ikke andre divisorer end de trivielle -- sådanne tal kaldes primtal. Vi kan formalisere definitionen:
De første primtal er den kendte talfølge
![]() .
Et tal som ikke er et primtal, kaldes et sammensat tal. Har vi
to tal som ikke har nogle fælles, ægte divisorer, siger vi at de er
indbyrdes primiske. Der gælder så følgende om et sammensat tal:
.
Et tal som ikke er et primtal, kaldes et sammensat tal. Har vi
to tal som ikke har nogle fælles, ægte divisorer, siger vi at de er
indbyrdes primiske. Der gælder så følgende om et sammensat tal:
Vi vil straks gå videre og vise den fundamentale sætning 1.3, som er taget fra [8, s. 14]:
| (1.1) |
Den mindste divisor i ![]() som er større end 1, vil så ifølge
sætning 1.2 være et primtal, som vi ikke havde
fundet endnu.
som er større end 1, vil så ifølge
sætning 1.2 være et primtal, som vi ikke havde
fundet endnu.
![]()
Med hensyn til Mersenne primtal, har man endnu ikke kunnet give noget bevis for, at der også er uendelig mange af dem[14, s. 80]. Man kan dog heller ikke give nogen god grund til, at det ikke skulle være tilfældet.
Hvis ![]() , så kan vi skrive
, så kan vi skrive ![]() som
som ![]() hvor
hvor ![]() er et
primtal.
er et
primtal. ![]() vil så også være en primfaktor i
vil så også være en primfaktor i ![]() , da
, da
![]() .
Hvis nu
.
Hvis nu ![]() , er vi færdige, ellers fortsætter vi på samme måde ved
at opløse
, er vi færdige, ellers fortsætter vi på samme måde ved
at opløse ![]() i
i ![]() .
.
Vi fortsætter indtil ![]() , hvilket vil ske på et tidspunkt, da vi
har en aftagende følge af positive hele tal:
, hvilket vil ske på et tidspunkt, da vi
har en aftagende følge af positive hele tal:
| (1.2) |
Efter at have fundet ![]() primtal, har vi fået opløst
primtal, har vi fået opløst ![]() i dets primfaktorer:
i dets primfaktorer:
![]() , hvilket var det vi skulle.
, hvilket var det vi skulle.
![]()
Der er forskellige måder hvorpå man kan vise, at et givent tal er et primtal.
Det simpleste er at prøve at finde en faktor til tallet ![]() ved
division. Sætning 1.2 siger, at hvis vi
kan finde en ægte divisor til tallet
ved
division. Sætning 1.2 siger, at hvis vi
kan finde en ægte divisor til tallet ![]() , så er
, så er ![]() ikke et primtal.
Kan vi omvendt vise, at der ikke findes nogen ægte divisorer, så er
tallet et primtal.
ikke et primtal.
Kan vi omvendt vise, at der ikke findes nogen ægte divisorer, så er
tallet et primtal.
Så vi starter med at prøve at dele med 2, og hvis det ikke går op,
prøver vi med 3, 4, 5 osv. Vi behøver kun at prøve indtil ![]() ,
hvor
,
hvor ![]() er det tal vi prøver med, da tal derover ikke vil kunne gå op
i
er det tal vi prøver med, da tal derover ikke vil kunne gå op
i ![]() . Hvis
. Hvis ![]() , hvor
, hvor ![]() , må
, må ![]() , men så er
, men så er ![]() allerede testet.
allerede testet.
Da man skal prøve med tal indtil ![]() , bliver beregningstiden
meget stor, når vi arbejder med store tal. Allerede i antikken havde
man derfor fundet en mere effektiv metode kaldet Eratosthenes
si.
, bliver beregningstiden
meget stor, når vi arbejder med store tal. Allerede i antikken havde
man derfor fundet en mere effektiv metode kaldet Eratosthenes
si.
Når man gerne vil finde alle primtal under en vis grænse ![]() , kan man
bruge en metode som går under navnet Eratosthenes si.
, kan man
bruge en metode som går under navnet Eratosthenes si.
Man starter med at skrive alle tallene mindre end ![]() og større end 1
op efter hinanden. Sætter vi
og større end 1
op efter hinanden. Sætter vi ![]() får vi følgende talrække:
får vi følgende talrække:
| (1.3) |
| (1.4) |
Det næste tal i listen er 3, kan ikke have nogen ægte divisor. Hvis det havde, ville 3 ikke længere være i listen. Vi fjerner så alle tal som har 3 som divisor:
| (1.5) |
Vi kommer så til tallet 5. Men da ![]() , behøver vi ikke at
fortsætte. Hvis der var flere sammensatte tal under 20, kunne det jo
ikke have et primtal mindre end 5 som faktor. Det mindste sammensatte
tal vi kunne “ramme” ville altså være 25. Fordelen ved denne metode
er, at vi finder mange primtal på én gang, ved at udføre næsten de
samme beregninger som ved det første metode.
, behøver vi ikke at
fortsætte. Hvis der var flere sammensatte tal under 20, kunne det jo
ikke have et primtal mindre end 5 som faktor. Det mindste sammensatte
tal vi kunne “ramme” ville altså være 25. Fordelen ved denne metode
er, at vi finder mange primtal på én gang, ved at udføre næsten de
samme beregninger som ved det første metode.
Da denne opgave skal handle om Mersenne primtal, må vi hellere slå fast hvad det er for primtal vi kalder Mersenne primtal, samt indføre en notation for dem:
| (1.6) |
Det var tidligere en normal misforståelse, at ![]() altid ville være
et primtal, bare
altid ville være
et primtal, bare ![]() var det. Men i 1536 viste Hudalricus
Regius[5], at det ikke var tilfældet, idet
var det. Men i 1536 viste Hudalricus
Regius[5], at det ikke var tilfældet, idet
![]() .
.
Pietro Cataldi fandt i 1588 ud af, at
![]() og
og
![]() . Men han mente også at
. Men han mente også at
![]() ,
,
![]() og
og
![]() var
primtal.1.1
var
primtal.1.1
Det kendetegner disse første forsøg på et finde store primtal, at man
ikke havde ret hver gang. Men det er ikke så underligt, for man skal
jo huske at f.eks.
![]() jo har 10 cifre. Det er nogle
enorme tal at arbejde med, hvis man ikke har elektroniske
hjælpemidler.1.2
jo har 10 cifre. Det er nogle
enorme tal at arbejde med, hvis man ikke har elektroniske
hjælpemidler.1.2
Man fortsatte med at lede efter endnu større primtal, og i 1644 påstod
den franske munk Marin Mersenne (1588-1648) i sin bog
Cogitata Physica-Mathematica at ![]() var et primtal for
var et primtal for
| (1.7) |
I denne liste var det kun tallene fra 31 og op efter, man var i tvivl om. Mersenne indrømmede endda at han ikke havde testet alle disse tal, men da tallene er så store, kunne ingen modbevise ham.
Først over 100 år senere kunne L. Euler (1707-1783) vise at ![]() virkelig er et primtal, og 230 år senere viste E. Lucas (1842-1891)
at
virkelig er et primtal, og 230 år senere viste E. Lucas (1842-1891)
at ![]() også er et primtal.
også er et primtal. ![]() har 39 cifre og er det
største primtal som er fundet ved håndkraft.
har 39 cifre og er det
største primtal som er fundet ved håndkraft.
Senere fandt man ud af, at Mersenne havde glemt 3 tal, nemlig
![]() ,
, ![]() og
og ![]() . Han tog også fejl ved
. Han tog også fejl ved
![]() .1.3 Men hans navn blev alligevel knyttet til disse primtal.
.1.3 Men hans navn blev alligevel knyttet til disse primtal.
Det beviser vi nu, beviset er fra [4].
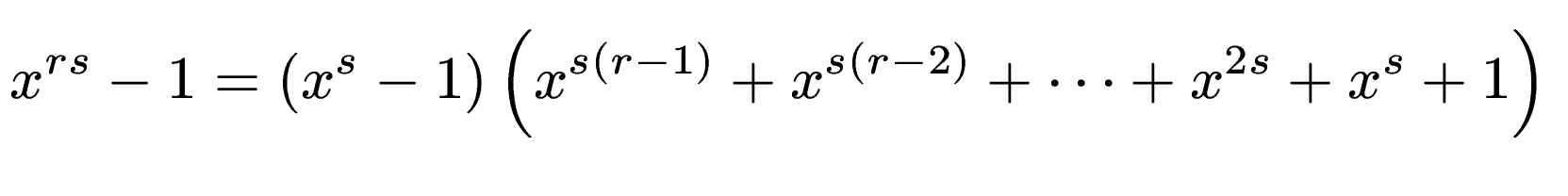 |
(1.8) |
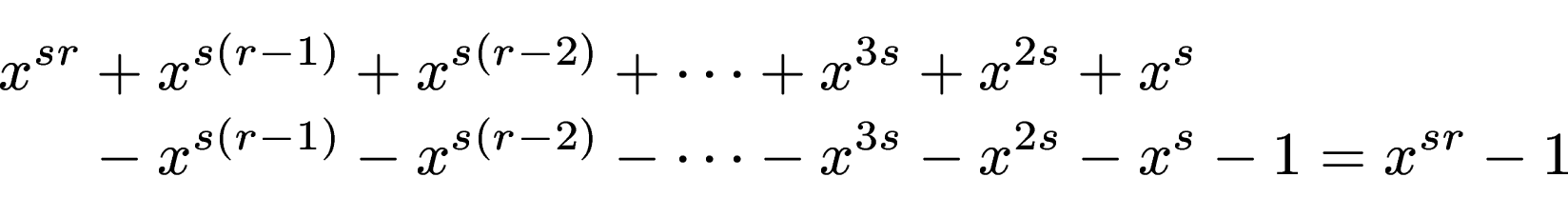 |
(1.9) |
Vi har nu vist at ![]() ikke kan være et primtal, hvis
ikke kan være et primtal, hvis ![]() ikke selv
er et primtal. Vi har nemlig vist at tallet
ikke selv
er et primtal. Vi har nemlig vist at tallet ![]() går op i
går op i ![]() ,
hvis
,
hvis ![]() kan skrives som
kan skrives som ![]() .
.
![]()
Sætning 1.6 fortæller os, at vi nemt kan finde
faktorer til ![]() , når
, når ![]() ikke er et primtal. F.eks. må
ikke er et primtal. F.eks. må
![]() være en faktor i
være en faktor i
![]() , ligesom
, ligesom ![]() må være
det.
må være
det.
Hvis ![]() ikke er et primtal, kan vi faktisk udtale os om
formen af divisorerne:
ikke er et primtal, kan vi faktisk udtale os om
formen af divisorerne:
| (1.10) |
Jeg giver ikke noget bevis for sætning 1.7, i stedet henvises til [6].
Perfekte tal er rimelig sjældne. Man kender også kun lige
perfekte tal, men har endnu ikke kunne give noget bevis hverken for
eller imod, at der skulle findes et ulige perfekt tal. Men man ved at
et eventuelt ulige perfekt tal må være stort[11, s. 167], da
man ved hjælp af computere har undersøgt alle tal op til ![]() !
!
Hvert Mersenne primtal vi finder, giver os samtidig et lige perfekt tal[14, s. 81] ifølge sætning 1.9:
Før vi kan bevise sætning 1.9 må vi først
introducere funktionen ![]() , se [7]:
, se [7]:
Der er lige en lille sætning vi også skal bruge, beviset for sætningen har jeg selv lavet:
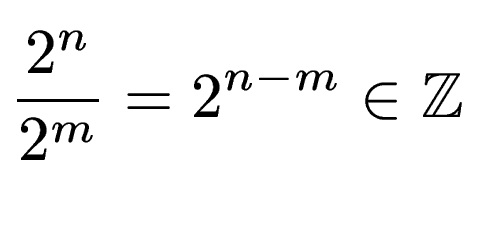 |
(1.12) |
Divisorerne er altså
![]() . Deres
sum er:
. Deres
sum er:
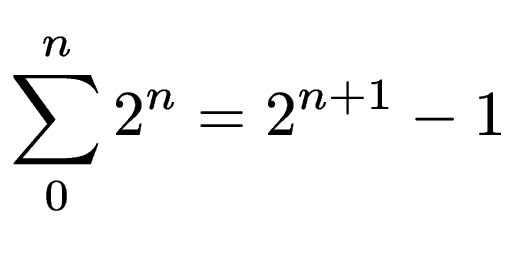 |
(1.13) |
Vi kan så bevise sætning 1.9 som i [3]:
Vi har altså:
| (1.14) |
Vi kan også vise at det omvendte gælder, nemlig at hvis ![]() er et lige
perfekt tal, så vil det kunne skrives som
er et lige
perfekt tal, så vil det kunne skrives som
![]() .
.
Vi har altså et lige perfekt tal, ![]() . Det må vi kunne skrive som
. Det må vi kunne skrive som
![]() hvor
hvor ![]() og
og ![]() er et ulige heltal. Vi regner nu på
er et ulige heltal. Vi regner nu på
![]() :
:
| (1.15) |
| (1.16) |
Vi ved også at ![]() er et perfekt tal:
er et perfekt tal:
| (1.17) |
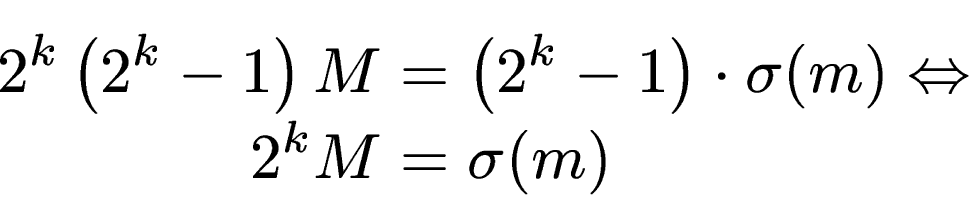 |
(1.20) |
| (1.21) |
Vi har altså at ![]() er et primtal. Tallet
er et primtal. Tallet ![]() får så formen
får så formen
![]() , hvilket var det vi skulle vise.
, hvilket var det vi skulle vise.
![]()
Som et eksempel på brugen af sætning 1.9, kan vi se
at tallet
![]() er et perfekt tal, da
er et perfekt tal, da
![]() er et primtal.
er et primtal.
Når man regner med kongruenser, regner man faktisk med rester efter divisioner. Derfor er kongruensbegrebet uhyre vigtigt i forbindelse med primtal, da man netop i denne sammenhæng ofte beskæftiger sig med brøker, rester og tals delelighed generelt.
Vi starter med at definere kongruens:
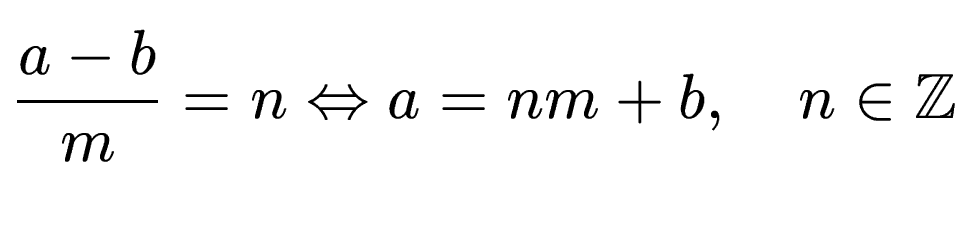 |
(2.2) |
Det var C. F. Gauss (1777-1855) som opfandt denne notation[11, s. 69]. Notationen ligner den vi bruger til almindelige ligninger, og det viser sig at man kan regne på kongruenserne efter nogle specielle regler. Det var et stort fremskridt, da man nu havde fået et værktøj til at beskrive de ting, der sker når tal går op i hinanden.
Da de fleste af de følgende sætninger er ret trivielle at bevise,
har jeg flyttet beviserne over i bilaget, se
side ![]() .
.
Vi kan så gange igennem med
![]() , og får så at
, og får så at
![]() hvilket viser at
hvilket viser at ![]() er kongruent
med
er kongruent
med ![]() modulus
modulus
![]() .
.
![]()
Som et eksempel kan vi se på kongruensen
![]() . Her har vi at største fælles divisor for 6 og 15 lig 3. Vi
kan derfor omskrive kongruensen til
. Her har vi at største fælles divisor for 6 og 15 lig 3. Vi
kan derfor omskrive kongruensen til
![]() , hvilket
tydeligvis også er sandt.
, hvilket
tydeligvis også er sandt.
Har vi en ligning som
![]() får vi en hel række løsninger, da
får vi en hel række løsninger, da
![]() . Det at vi får en
hel klasse af løsninger, fører os over i begrebet
restklasser:
. Det at vi får en
hel klasse af løsninger, fører os over i begrebet
restklasser:
Ud fra definitionen og det vi ved om kongruens, kan vi skrive at ![]() og
og
![]() ligger i samme restklasse modulus
ligger i samme restklasse modulus ![]() sådan her:
sådan her:
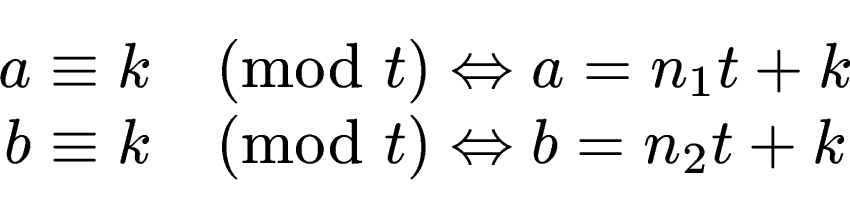 |
(2.3) |
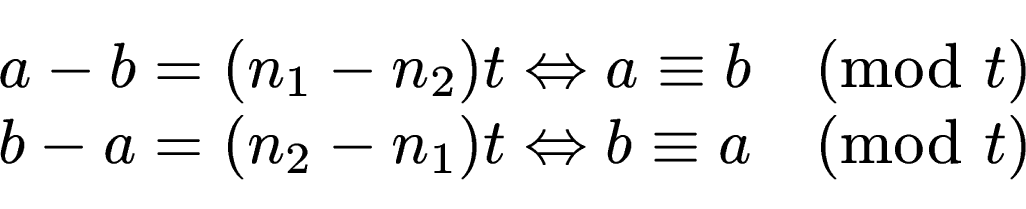 |
(2.4) |
Gruppeteorien beskæftiger sig med forskellige mængder af objekter, som er knyttet sammen af kompositioner, som opfylder nogle bestemte krav. Da der ikke er nogle bestemte krav til typen af objekter, er gruppeteori altså en del af det man vil kalde abstrakt algabra.
Man skal lægge mærke til at symbolet ![]() ikke er brugt som et
gangetegn.
ikke er brugt som et
gangetegn. ![]() angiver blot en vilkårlig forskrift, som f.eks. kunne
være givet ved
angiver blot en vilkårlig forskrift, som f.eks. kunne
være givet ved
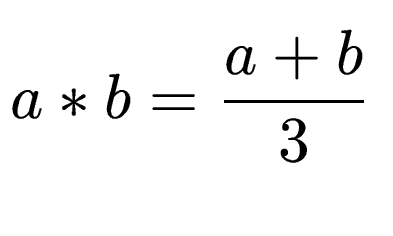 |
(3.1) |
Ud fra en komposition får vi så en algebraisk struktur:
Vi kan nu se, at vi allerede kender mange algebraiske strukturer.
F.eks. har vi at
![]() er en algebraisk struktur, da der
gælder
er en algebraisk struktur, da der
gælder
| (3.2) |
Næste skridt ville så være at fastlægge, hvordan vi ville regne med elementerne i en algebraisk struktur. Men da disse regler blot er udtryk for en mere formel beskrivelse af de regler vi allerede kender, er de flyttet til bilaget, se afsnit C.1. Vi vil dog lige ridse definitionerne op:
For at den associative lov er opfyldt for kompositionen ![]() ,
skal der gælde følgende
,
skal der gælde følgende
| (3.3) |
Vi har også den kommutative lov:
| (3.4) |
I nogle algebraiske strukturer findes et element som er neutralt.
| (3.5) |
Ved addition kaldes det neutrale element for et nul-element mens det kaldes et et-element ved multiplikation.
Når vi så har en vilkårlig semigruppe med et neutralt element, kan vi definere et omvendt element:
| (3.6) |
Hvis kompositionen ![]() også er kommutativ, siges gruppen at være
kommutativ. En kommutativ gruppe kaldes også en abelsk
gruppe.3.1
også er kommutativ, siges gruppen at være
kommutativ. En kommutativ gruppe kaldes også en abelsk
gruppe.3.1
Vi ser nu hvorfor man kalder en associativ algebraisk struktur for en semigruppe, idet en semigruppe kun mangler at opfylde de to sidste punkter.
Både de enkelte elementer i en gruppe og gruppen selv kan have det vi betegner med orden. Vi definerer et elements orden således:
| (3.7) |
Vi vil nu bevise at ethvert element i en endelig gruppe har en orden
| (3.8) |
Vi går ud fra at det ikke er muligt. For at undgå at komme til det neutrale element, må man altså kunne cykle i ring blandt gruppens elementer. Da gruppen indeholder et endeligt antal elementer, vil man før eller siden komme tilbage til et element, man har været ved før.
Dette element må endvidere være det oprindelige element ![]() . Hvis
ikke, skulle der være to forskellige løsninger til ligningen
. Hvis
ikke, skulle der være to forskellige løsninger til ligningen
![]() , hvor
, hvor ![]() er det første element, vi har været ved
før.
er det første element, vi har været ved
før.
Vi har altså at
![]() . Det er lovligt at tilføje
. Det er lovligt at tilføje
![]() på hver side af lighedstegnet, så det gør vi. Det giver os
at
på hver side af lighedstegnet, så det gør vi. Det giver os
at
![]() . Vi ser nu
at vi alligevel når til det neutrale element, nemlig efter
. Vi ser nu
at vi alligevel når til det neutrale element, nemlig efter ![]() gange.
gange.
![]()
En gruppe har også en orden:
Beviset kommer fra [11, s. 173]:
Ifølge definitionen ef et elements orden (sætning 3.8)
må
![]() nu være mindre end eller ligmed
nu være mindre end eller ligmed ![]() , som selv er mindre
end eller lig med
, som selv er mindre
end eller lig med ![]() :
:
![]() . Det giver os at
. Det giver os at
![]() .
.
![]()
Dette bevis stammer også fra [11, s. 173]:
| (3.11) |
Hvis nu ![]() har vi fundet en mindre eksponent end
har vi fundet en mindre eksponent end ![]() som giver os
det neutrale element, da
som giver os
det neutrale element, da ![]() . Dette strider imod definitionen af et
elements orden, som jo siger at
. Dette strider imod definitionen af et
elements orden, som jo siger at ![]() er den mindste eksponent for
hvilken det gælder at
er den mindste eksponent for
hvilken det gælder at
![]() . Derfor kan
. Derfor kan ![]() kun være 0, hvilket
giver os at
kun være 0, hvilket
giver os at
| (3.12) |
Følgende sætning bruges i beviset af Lucas-Lehmer sætningen.
Vi mangler så blot at vise,
![]() . Vi
tager to elementer fra
. Vi
tager to elementer fra ![]() ,
, ![]() og
og ![]() , som er invertible, med de
inverse elementer
, som er invertible, med de
inverse elementer ![]() og
og ![]() . Det inverse element til
. Det inverse element til ![]() er så
er så
![]() , hvilket vi kan vise ved brug af den associative
lov:
, hvilket vi kan vise ved brug af den associative
lov:
| (3.13) |
Lucas-Lehmer sætningen bruges til at bevise at et givent Mersenne tal er et primtal. Derfor omtaler jeg den også sommetider som Lucas-Lehmer testen.
Det følgende bevis for Lucas-Lehmer sætningen er taget fra [11, s. 170-173], som har det fra [2]. Oprindeligt stammer beviset fra [15].
| (4.1) |
Der gælder nu følgende om serien ![]() ,
, ![]() og
og
![]() :
:
Ifølge (4.2) er ![]() . Vi ser at
. Vi ser at
![]() også er lig
også er lig ![]() .
.
Vi viser så, at hvis (4.3) er sand for ![]() , så
er den også sand for
, så
er den også sand for ![]() .
. ![]() skal så være lig
skal så være lig
![]() :
:
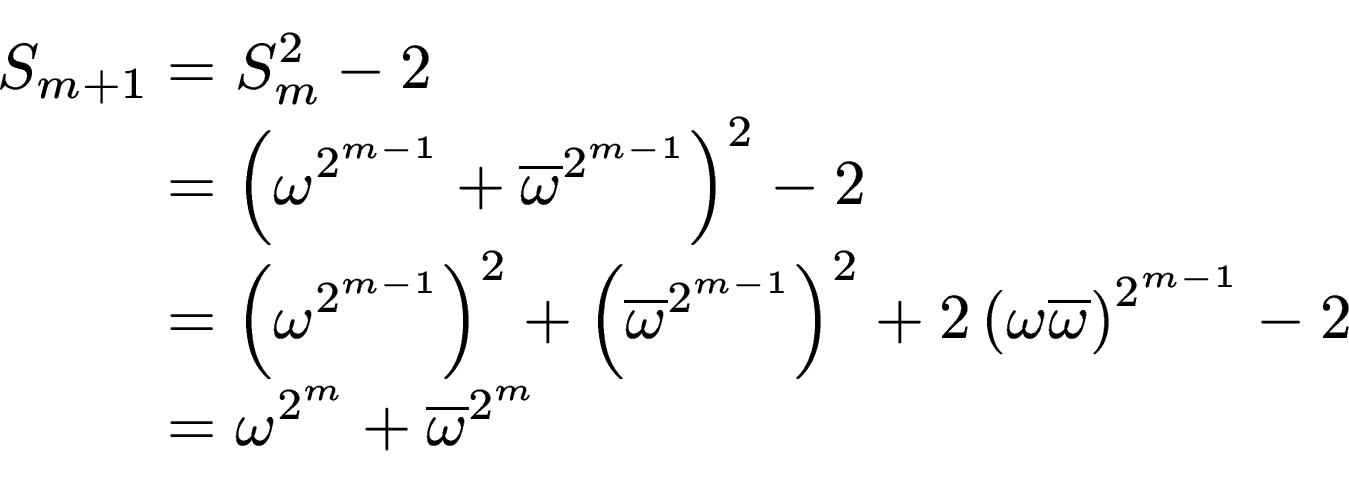 |
(4.4) |
Vi har nu vist at (4.3) gælder for både ![]() og for
og for ![]() , derfor gælder den for alle
, derfor gælder den for alle
![]() .
.
![]()
Vi går nu ud fra at ![]() går op i
går op i ![]() , og ud fra
sætning 4.2 får vi at det må betyde følgende:
, og ud fra
sætning 4.2 får vi at det må betyde følgende:
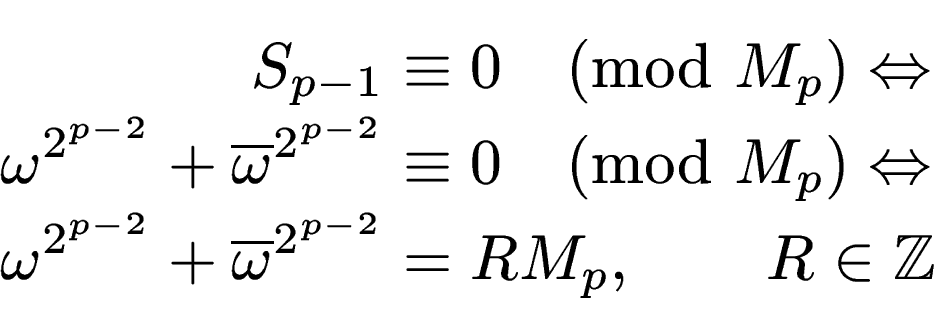 |
(4.5) |
I sidste linie skrev vi kongruensen som en normal ligning. Denne
arbejder vi videre på, først ganger vi igennem med
![]() og vi flytter 1 over på højresiden:
og vi flytter 1 over på højresiden:
Vi får brug for (4.6) og (4.7) lidt senere.
Vi vil gå ud fra at ![]() ikke er et primtal, og vil vise at
dette medfører en modstrid. Hvis
ikke er et primtal, og vil vise at
dette medfører en modstrid. Hvis ![]() ikke er et primtal, vil der
være en primfakter
ikke er et primtal, vil der
være en primfakter ![]() som opfylder at
som opfylder at
![]() .
.
Vi lader nu
![]() betegne mængden af heltal modulus
betegne mængden af heltal modulus ![]() og
og
![]() betegne mængden
betegne mængden
![]() . Vi
definerer to kompositioner på mængden
. Vi
definerer to kompositioner på mængden ![]() , addition og multiplikation.
I begge tilfælde reducerer vi koefficienterne med modulus
, addition og multiplikation.
I begge tilfælde reducerer vi koefficienterne med modulus ![]() .
.
Addition defineres på normal vis:
| (4.8) |
| (4.9) |
Det neutrale element i ![]() med hensyn til multiplikation er
med hensyn til multiplikation er
![]() . Da der ifølge sætning C.6 højst
findes ét neutralt element, er det nok at gøre prøve med
. Da der ifølge sætning C.6 højst
findes ét neutralt element, er det nok at gøre prøve med
![]() for at vise at det virkeligt er det neutrale element:
for at vise at det virkeligt er det neutrale element:
| (4.10) |
Vi lader ![]() betegne gruppen af invertible elementer i
betegne gruppen af invertible elementer i ![]() . Ved at
bruge sætning 3.12 ser vi at
. Ved at
bruge sætning 3.12 ser vi at ![]() er en gruppe.
er en gruppe.
Vi ser nu på
![]() som et element i
som et element i ![]() .
. ![]() er
også et element i
er
også et element i ![]() da det er invertibelt:
da det er invertibelt:
![]() . Hvis man tænker nærmere over det, vil det
først se ud som om at
. Hvis man tænker nærmere over det, vil det
først se ud som om at
![]() ikke er et
element i
ikke er et
element i ![]() . Alle elementerne i
. Alle elementerne i ![]() har jo formen
har jo formen
![]() hvor
hvor
![]() . Koefficienterne skulle
altså ikke være negative.
. Koefficienterne skulle
altså ikke være negative.
Men da koefficienterne bliver reduceret modulus ![]() , kan de i
virkeligheden have denne form:
, kan de i
virkeligheden have denne form:
| (4.11) |
Vi valgte ![]() så det gik op i
så det gik op i ![]() . Derfor gælder der at
. Derfor gælder der at
| (4.12) |
Set som et element i ![]() er
er
![]() altså lig 0, da
koefficienterne reduceres modulus
altså lig 0, da
koefficienterne reduceres modulus ![]() . Ud fra det kan vi omskrive
ligningerne (4.6) og (4.7) til:
. Ud fra det kan vi omskrive
ligningerne (4.6) og (4.7) til:
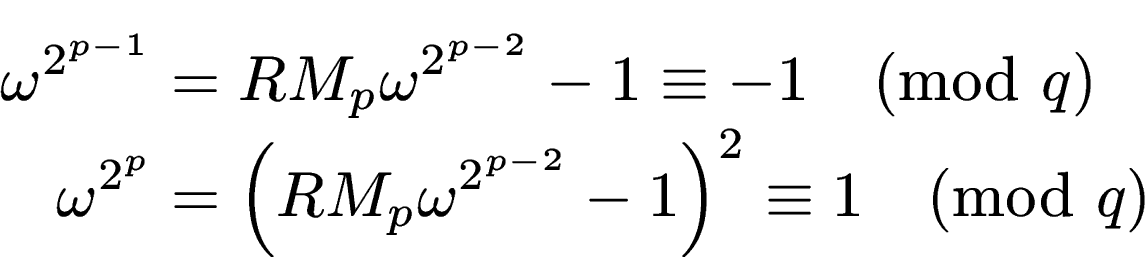 |
(4.13) |
Set som et element i ![]() får vi altså at
får vi altså at
Da
![]() har vi ifølge
sætning 3.11 at
har vi ifølge
sætning 3.11 at
![]() går op i
går op i ![]() . Vi
har altså at
. Vi
har altså at
![]() hvor
hvor ![]() . Hvis vi kvadrerer
. Hvis vi kvadrerer
![]() får vi
får vi
![]() . Bliver vi ved med
at kvadrere får vi til sidst at
. Bliver vi ved med
at kvadrere får vi til sidst at
![]() , hvilket er
falsk i følge (4.14). Derfor kan
, hvilket er
falsk i følge (4.14). Derfor kan ![]() ikke være
mindre end
ikke være
mindre end ![]() , hvilket giver os at
, hvilket giver os at
![]() .
.
Da ![]() består af alle de invertible elementer fra
består af alle de invertible elementer fra ![]() , får vi at
, får vi at
![]() . Der er nemlig
. Der er nemlig ![]() elementer i
elementer i
![]() , og
vi bruger 2 elementer til hvert element i
, og
vi bruger 2 elementer til hvert element i ![]() . Det giver os at der er
. Det giver os at der er
![]() elementer i
elementer i ![]() . Men da elementet
. Men da elementet
![]() ikke er
invertibelt, findes der højst
ikke er
invertibelt, findes der højst ![]() elementer i
elementer i ![]() .
.
![]() er et element i
er et element i ![]() , da
, da
![]() . Her er
det at
. Her er
det at
![]() , så der gælder at både
, så der gælder at både ![]() og
og ![]() er elementer i
er elementer i
![]() . Vi får så ifølge
sætning 3.10 at
. Vi får så ifølge
sætning 3.10 at
Sætter vi nu (4.15) sammen med (4.16) får vi følgende modstrid:
| (4.17) |
Vi har nu vist at ![]() ikke kan være en primfaktor i
ikke kan være en primfaktor i ![]() . Da vi netop
valgte
. Da vi netop
valgte ![]() , så det ville være primfaktor, må det betyde at
, så det ville være primfaktor, må det betyde at ![]() ikke
har nogen primfaktorer overhoved --
ikke
har nogen primfaktorer overhoved -- ![]() må derfor være et primtal.
må derfor være et primtal.
![]()
Nu da vi har vist at Lucas-Lehmer sætningen kan bruges til at afgøre
om et givent tal på formen ![]() er et primtal, ville det være
oplagt at benytte testen i et computerprogram.
er et primtal, ville det være
oplagt at benytte testen i et computerprogram.
Der er i øjeblikket en koordineret jagt igang efter meget store Mersenne primtal, kaldet GIMPS. GIMPS er en forkortelse for “The Great Internet Mersenne Prime Search”, og som navnet siger foregår eftersøgninger på tværs af Internettet. Omkring 35.000 maskiner hjælper med i projektet[10].
Det foregår sådan, at der kører et program på hver computer der er tilmeldt projektet. Dette program aftaler med en central server, at det undersøger en bestemt eksponent. Den centrale server holder styr på, hvilke eksponenter der stadig er ledige, hvilke der allerede er tjekket én gang osv. På den måde arbejder de mange computere sig efterhånden gennem større og større eksponenter.
Min egen computer har netop afsluttet en test af
![]() , som
ikke var et primtal. Den er nu igang med
, som
ikke var et primtal. Den er nu igang med
![]() . Selv om
Lucas-Lehmer testen er meget effektiv i forhold til andre metoder,
tager det alligevel omkring en måned at teste bare én eksponent. Og
det er endda på en hurtig maskine.
. Selv om
Lucas-Lehmer testen er meget effektiv i forhold til andre metoder,
tager det alligevel omkring en måned at teste bare én eksponent. Og
det er endda på en hurtig maskine.
Men GIMPS har alligevel testet omkring 225.000 eksponenter igennem de 4 år projektet har været igang. Alle eksponenter mindre end 3.210.800 er nu dobbelttjekket, og alle under 5.558.700 er tjekket mindst én gang[17].
Det program som leder efter Mersenne primtallene hedder
mprime. Da det trods alt er en tidskrævende proces at
gennemføre en Lucas-Lehmer test, prøver man på at undgå den. Man
starter derfor med at prøve at finde en faktor ved
division[16]. Man bruger en modificeret udgave af
Eratosthenes si (se afsnit 1.2.2), hvor alle
potentielle faktorer på formen ![]() bliver repræsenteret. Man
prøver derefter at dividere Mersenne tallet med de divisorer som ikke
blev siet fra.
bliver repræsenteret. Man
prøver derefter at dividere Mersenne tallet med de divisorer som ikke
blev siet fra.
Man laver ikke bare en “normal” division, men bruger en meget hurtig algoritme. Da selve algoritmen blot er en beskrivelse af implementeringen i computeren, har jeg lagt den om i bilaget, se bilag D.
Hvis man ikke finder nogen divisorer, må man lave en Lucas-Lehmer
test. Sætning 4.1 siger at tallet ![]() er et
primtal hvis det går op i
er et
primtal hvis det går op i ![]() .
.
Vi skal altså finde ud af om
![]() . Men hvis
vi bare begynder at regne
. Men hvis
vi bare begynder at regne ![]() ud, får vi hurtigt nogle
meget store tal (
ud, får vi hurtigt nogle
meget store tal (
![]() ), hvilket vi ikke er
interesseret i, da disse er langsomme at arbejde med.5.1
), hvilket vi ikke er
interesseret i, da disse er langsomme at arbejde med.5.1
Derfor regner vi modulus ![]() , sådan at vi efter hvert trin
reducerer
, sådan at vi efter hvert trin
reducerer ![]() modulus
modulus ![]() . Det kan vi gøre, fordi hvis
. Det kan vi gøre, fordi hvis
| (5.1) | ||
så har vi ifølge sætning 2.5 at | ||
| (5.2) | ||
og vi kan så trække 2 fra på begge sider | ||
| (5.3) | ||
Hvis vi efter sidste trin får resten 0, ved vi at ![]() er et
primtal. Vi demonstrere det ved at vise at
er et
primtal. Vi demonstrere det ved at vise at ![]() virkeligt er et
primtal. Processen skal så igennem
virkeligt er et
primtal. Processen skal så igennem ![]() trin. Ved hvert trin
bruger man resten fra sidste trin, kvadrerer den og trækker 2 fra, og
finder en ny rest:
trin. Ved hvert trin
bruger man resten fra sidste trin, kvadrerer den og trækker 2 fra, og
finder en ny rest:
| 0 |
Alle eksponenter bliver dobbelttjekket for at sikre sig mod fejl, som kan opstå undervejs i den lange Lucas-Lehmer test. Det er ikke selve algoritmen som fejler noget, men i stedet de moderne processorer. Man bruger kommatal (floating points på engelsk) til beregningerne, da processorerne er hurtigere til disse beregninger, end til heltalsberegninger. Men der kan så opstå afrundingsfejl undervejs.
Derfor gemmer man de sidste 64 bit af ![]() efter en test, og når
så dobbelttjekket er færdigt, sammenligner man disse bit fra de to
test. Hvis disse to tal er ens, er begge programmer altså nået frem
til det samme tal for
efter en test, og når
så dobbelttjekket er færdigt, sammenligner man disse bit fra de to
test. Hvis disse to tal er ens, er begge programmer altså nået frem
til det samme tal for ![]() , og eksponenten bliver så erklæret for
testet. Det sker sommetider at de to tal ikke stemmer, og så må man
igang med en tredje test. Fejlraten på en Lucas-Lehmer test er ifølge
[16] lidt over 1%.
, og eksponenten bliver så erklæret for
testet. Det sker sommetider at de to tal ikke stemmer, og så må man
igang med en tredje test. Fejlraten på en Lucas-Lehmer test er ifølge
[16] lidt over 1%.
Vi startede med en gennemgang af Mersenne primtallenes historie, og kom i den forbindelse ind på hvor svært det var dengang at afgøre om Marin Mersenne havde ret eller ej.
Jeg har vist hvordan man kan bruge forskellige metoder til at vise at et givent tal er et primtal. Vi så hvordan de fleste metoder er besværlige at bruge, da der skal udføres mange beregninger med store tal.
De nødvendige forudsætninger for beviset af Lucas-Lehmer sætningen blev gennemgået, og sætningen blev da også bevist.
Endelig blev der givet et eksempel på, hvordan man bruger Lucas-Lehmer sætningen i vore dage til at finde meget store primtal.
Jeg synes, at det er lykkedes at vise, hvordan tingene hænger sammen på kryds og tværs af matematikkens grene. Mange spændende aspekter ved kongruenser og grupper er blevet vist og forklaret. Gruppeteori er et interessant emne, da argumenterne ofte bygger på små og i sig selv simple ting, selv deres resultater kan være vidtgående.
Det samme gælder for kongruenser. Med modulusregning har vi et værktøj, hvormed vi nu kan beskrive en masse af det vi allerede viste om tal og deres indbyrdes forhold. Vi kan beskrive det på en fornuftig måde så man kan arbejde systematisk videre med det.
Vi har også set hvor svært det er at finde meget store primtal -- og alligevel har man fundet et tal med over 2 millioner cifre ved at bruge Lucas-Lehmer testen.
Tabel A.1 indeholder en komplet list over de 38
Mersenne primtal man har fundet hidtil. Tabellen er hentet fra
[5]. Grunden til at det 38. tal står på listen som
“??” er, at man endnu ikke har tjekket alle tal mellem
![]() og
og
![]() . Det kan godt tænkes at der gemmer sig endnu et tal i
intervallet.
. Det kan godt tænkes at der gemmer sig endnu et tal i
intervallet.
Tabellen indeholder også antallet af cifre i Mersenne primtallet
![]() , så man kan se hvor imponerende store de er. Det perfekte tal
, så man kan se hvor imponerende store de er. Det perfekte tal
![]() er også taget med.
er også taget med.
Man kan f.eks. lægge mærke til hvor mange cifre der er i ![]() ,
som blev fundet i 1876 af Lucas, ved håndkraft. De efterfølgende
Mersenne primtal er alle fundet ved brug af elektroniske hjælpemidler.
,
som blev fundet i 1876 af Lucas, ved håndkraft. De efterfølgende
Mersenne primtal er alle fundet ved brug af elektroniske hjælpemidler.
Her er beviser til sætningerne 2.2 til 2.8.
Vi kan derfor lave følgende omskrivning
![]() . Sidste kongruens er sand, da
. Sidste kongruens er sand, da ![]() selvfølgelig går
op i
selvfølgelig går
op i ![]() til sidst med
til sidst med ![]() som rest.
som rest.
![]()
Som omtalt på side ![]() , vil vi her definere de
regneregler som gælder for algebraiske strukturer og derved også for
grupper.
, vil vi her definere de
regneregler som gælder for algebraiske strukturer og derved også for
grupper.
Vi vil nu fastlægge de normale regneregler i forbindelse med algebraiske strukturer og deres kompositioner. Vi starter med at definere at
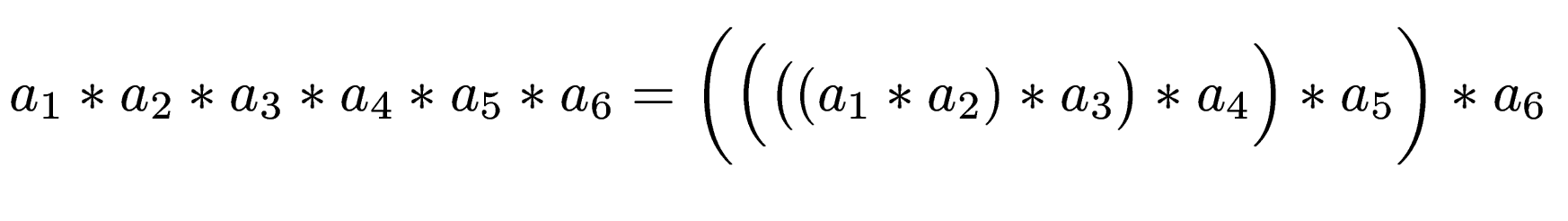 |
(C.1) |
Vi vil gerne have en kortere måde at skrive
![]() på,
og introducerer derfor skrivemåde
på,
og introducerer derfor skrivemåde
| (C.2) |
| (C.3) |
Den associative lov, se definition 3.3, siger, at vi
kan sætte og hæve parenteser i et udtryk med 3 led, uden at værdien af
udtrykket ændrer sig. Følgende sætning, som er taget fra [13, s.
137], udtaler sig om tilfældet hvor der er ![]() led
led
| (C.4) |
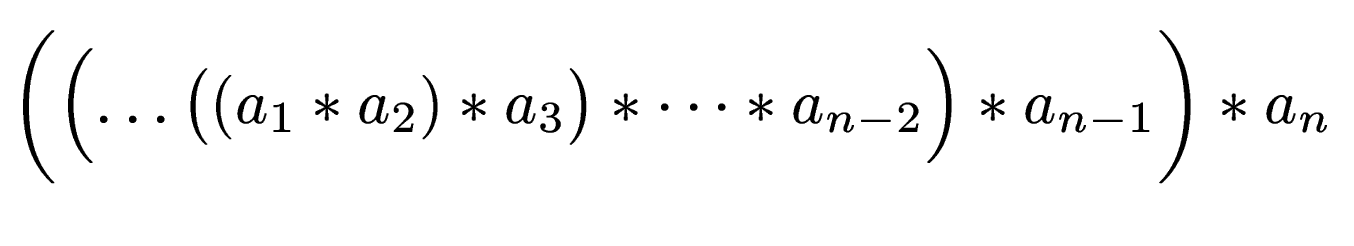 |
(C.5) |
Vi kan sætte parenteser omkring to vilkårlige naboled ![]() og
og
![]() på denne måde, da der altid vil være en underforstået
parentes, som slutter mellem
på denne måde, da der altid vil være en underforstået
parentes, som slutter mellem ![]() og
og ![]() . Denne parentes kan
fjernes, samtidig med at vi sætter en parentes omkring
. Denne parentes kan
fjernes, samtidig med at vi sætter en parentes omkring ![]() og
og
![]() .
.
![]()
Nu da vi har vist at vi kan sætte parenteser som vi vil i forbindelse med en associativ komposition, kan vi hurtigt bevise de regler, som ligger til grund for regning med potenser[13, s. 137]:
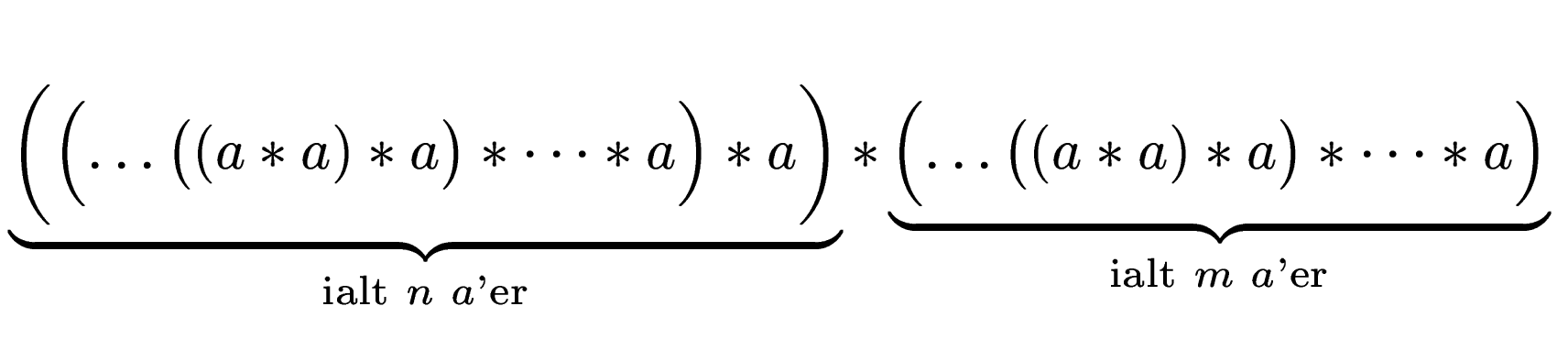 |
(C.7) |
Hæver vi alle parenteserne, får vi som ønsket
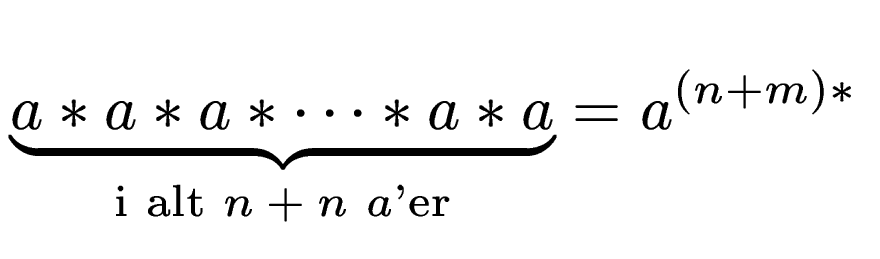 |
(C.8) |
Sætning C.4 kan direkte overføres til vores normale
potensregler, da
![]() udgør en semigruppe idet multiplikation
er associativ:
udgør en semigruppe idet multiplikation
er associativ:
![]() .
.
Når både den associative og den kommutative lov (se definition 3.4) er opfyldt, gælder der følgende sætning:
| (C.9) |
Ved gentagne gange at bytte rundt på leddene, kan vi altså ændre
rækkefølgen af leddene til en hvilken som helst rækkefølge vi er
interesseret i, uden at ændre på værdien af udtrykket.
![]()
Når man snakker om et neutralt element, se definition 3.5, kan man vise at
Dette bevis kommer fra[13, s. 140]:
| (C.10) |
Derved har vi vist, at der højst findes ét unikt neutralt element i
en algebraisk struktur.
![]()
Det viser sig, at der ligesom ved det neutrale element, højst findes
ét inverst element, se definition 3.6, til et
givent ![]() :
:
Hvis der finde to løsninger, ![]() og
og ![]() , må der gælde
følgende om dem:
, må der gælde
følgende om dem:
| (C.12) |
Trinnene i algoritmen er:
| (D.1) |
Vi prøver os frem og finder at
![]() og
og
![]() er mulige divisorer, da der gælder at
er mulige divisorer, da der gælder at
![]() og
og
![]() . Vi starter med
. Vi starter med ![]() .
.
Første trin i algoritmen er at skrive eksponenten som et binært tal:
![]() . De små mærker forneden angiver talsystemet. Vi
starter med 1 som vi kvadrerer. Vi ser så på den mest betydende bit i
eksponenten som er 1, hvilket betyder at vi skal gange med 2 og
finder resten ved division med 175. Resten bliver så 2.
. De små mærker forneden angiver talsystemet. Vi
starter med 1 som vi kvadrerer. Vi ser så på den mest betydende bit i
eksponenten som er 1, hvilket betyder at vi skal gange med 2 og
finder resten ved division med 175. Resten bliver så 2.
Vi gentager proceduren, og får denne gang at
![]() . Vi ganger med 2, da den næste bit også er 1. Fortsætter
vi, kan vi udfylde et skema som det i tabel D.1.
. Vi ganger med 2, da den næste bit også er 1. Fortsætter
vi, kan vi udfylde et skema som det i tabel D.1.
Tabel D.1 fortæller os at den sidste rest blev 137. Det
betyder at
![]() . Trækker vi en fra på begge
sider, får vi at
. Trækker vi en fra på begge
sider, får vi at
![]() . 175 er altså ikke
en faktor i
. 175 er altså ikke
en faktor i ![]() . Prøver vi så i stedet med den mulige divisor
233, får vi de udregninger som findes i tabel D.2.
. Prøver vi så i stedet med den mulige divisor
233, får vi de udregninger som findes i tabel D.2.
Så fortæller tabel D.2 os at
![]() . Vi kan altså nu
konstatere at 233 er en faktor i
. Vi kan altså nu
konstatere at 233 er en faktor i ![]() , som så ikke kan være et
primtal.
, som så ikke kan være et
primtal.
Der er i opgaven brugt en række elektroniske kilder i form af sider fra Internettet. Følgende kilder findes derfor på den vedlagte diskette: [3], [4], [5], [6], [7], [10], [16] og [17].
Kilderne er navngivet med samme nummer som her i opgaven, f.eks har [3] fået filnavnet kilde3.html på disketten.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.48)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -dir singlefile -up_url /danish/mersenne/ -up_title Tilbage -split 0 main.tex
The translation was initiated by Martin Geisler on 2001-01-31