


Næste: 1.1.1 Uendelig mange primtal
Op: 1. Primtal og deres
Foregående: 1. Primtal og deres
Forskellige tal har forskellige divisorer. Ethvert helt tal 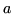 har de
såkaldte trivielle divisorer
har de
såkaldte trivielle divisorer 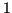 ,
, 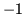 ,
, 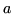 og
og 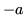 . Andre
divisorer kaldes ægte divisorer ifølge [13, s.
168].
. Andre
divisorer kaldes ægte divisorer ifølge [13, s.
168].
Nogle tal har ikke andre divisorer end de trivielle -- sådanne tal
kaldes primtal. Vi kan formalisere definitionen:
D
EFINITION 1.1
Et tal
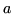
større end 1 som ikke har andre divisorer end
1,
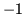
,
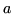
og
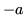
kaldes et
primtal.
De første primtal er den kendte talfølge
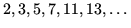 .
Et tal som ikke er et primtal, kaldes et sammensat tal. Har vi
to tal som ikke har nogle fælles, ægte divisorer, siger vi at de er
indbyrdes primiske. Der gælder så følgende om et sammensat tal:
.
Et tal som ikke er et primtal, kaldes et sammensat tal. Har vi
to tal som ikke har nogle fælles, ægte divisorer, siger vi at de er
indbyrdes primiske. Der gælder så følgende om et sammensat tal:
SÆTNING 1.2
Ethvert sammensat tal større end 1 har et primtal som
divisor, da den mindste divisor som er større end 1 er et primtal.
-
- Vi har et helt tal
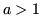 . Den mindste divisor i
. Den mindste divisor i 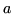 som er større end
1,
som er større end
1, 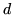 er så et primtal, da
er så et primtal, da 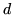 ikke har nogen ægte divisor. En ægte
divisor i
ikke har nogen ægte divisor. En ægte
divisor i 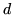 ville også være divisor i
ville også være divisor i 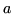 og samtidig være mindre
end
og samtidig være mindre
end 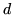 , hvilket ikke kan lade sig gøre, da
, hvilket ikke kan lade sig gøre, da 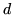 er den mindste ægte
divisor i
er den mindste ægte
divisor i 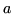 .
.

Underoverskrifter


 Copyright © 2001, Martin Geisler.
Copyright © 2001, Martin Geisler.
![]() har de
såkaldte trivielle divisorer
har de
såkaldte trivielle divisorer ![]() ,
, ![]() ,
, ![]() og
og ![]() . Andre
divisorer kaldes ægte divisorer ifølge [13, s.
168].
. Andre
divisorer kaldes ægte divisorer ifølge [13, s.
168].
![]() .
Et tal som ikke er et primtal, kaldes et sammensat tal. Har vi
to tal som ikke har nogle fælles, ægte divisorer, siger vi at de er
indbyrdes primiske. Der gælder så følgende om et sammensat tal:
.
Et tal som ikke er et primtal, kaldes et sammensat tal. Har vi
to tal som ikke har nogle fælles, ægte divisorer, siger vi at de er
indbyrdes primiske. Der gælder så følgende om et sammensat tal: