


Næste: D. Hurtig division
Op: C. Grupper
Foregående: C.3 Den kommutative lov
Når man snakker om et neutralt element, se
definition 3.5, kan man vise at
SÆTNING C.6
Der er højst ét neutralt element i en algebraisk struktur.
Dette bevis kommer fra[13, s. 140]:
-
- Hvis både
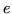 og
og 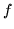 er neutrale elementer, så gælder der at
er neutrale elementer, så gælder der at
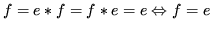 |
(C.10) |
Derved har vi vist, at der højst findes ét unikt neutralt element i
en algebraisk struktur.

Det viser sig, at der ligesom ved det neutrale element, højst findes
ét inverst element, se definition 3.6, til et
givent 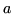 :
:
SÆTNING C.7
Der findes højst ét inverst element til
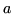
som opfylder ligningssystemet
 |
(C.11) |
-
- Som i beviset af det unikke neutrale element, vil vi vise at to
løsninger til ligningssystemet, i virkeligheden er den samme.
Hvis der finde to løsninger, 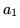 og
og 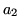 , må der gælde
følgende om dem:
, må der gælde
følgende om dem:
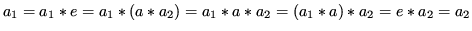 |
(C.12) |
Vi har her kun brugt den associative lov,C.1 som giver os mulighed for
frit at hæve og sætte parenteser. Det viste sig, at de to løsninger
var ens.

Fodnoter
- ... lov,C.1
- Vi arbejder i en
semigruppe, hvor kompositionen per definition er associativ.


 Copyright © 2001, Martin Geisler.
Copyright © 2001, Martin Geisler.
![]()
![]()
![]() :
:
![]() og
og ![]() , må der gælde
følgende om dem:
, må der gælde
følgende om dem: