Den associative lov, se definition 3.3, siger, at vi
kan sætte og hæve parenteser i et udtryk med 3 led, uden at værdien af
udtrykket ændrer sig. Følgende sætning, som er taget fra [13, s.
137], udtaler sig om tilfældet hvor der er ![]() led
led
| (C.4) |
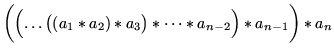 |
(C.5) |
Vi kan sætte parenteser omkring to vilkårlige naboled ![]() og
og
![]() på denne måde, da der altid vil være en underforstået
parentes, som slutter mellem
på denne måde, da der altid vil være en underforstået
parentes, som slutter mellem ![]() og
og ![]() . Denne parentes kan
fjernes, samtidig med at vi sætter en parentes omkring
. Denne parentes kan
fjernes, samtidig med at vi sætter en parentes omkring ![]() og
og
![]() .
.
![]()
Nu da vi har vist at vi kan sætte parenteser som vi vil i forbindelse med en associativ komposition, kan vi hurtigt bevise de regler, som ligger til grund for regning med potenser[13, s. 137]:
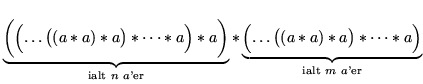 |
(C.7) |
Hæver vi alle parenteserne, får vi som ønsket
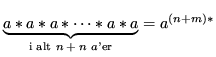 |
(C.8) |
Sætning C.4 kan direkte overføres til vores normale
potensregler, da
![]() udgør en semigruppe idet multiplikation
er associativ:
udgør en semigruppe idet multiplikation
er associativ:
![]() .
.