Næste: 5. Lucas-Lehmer sætningen i Op: 4. Lucas-Lehmer sætningen Foregående: 4. Lucas-Lehmer sætningen

4.1 Lucas-Lehmer

Det følgende bevis for Lucas-Lehmer sætningen er taget fra [11, s. 170-173], som har det fra [2]. Oprindeligt stammer beviset fra [15].

SÆTNING 4.1 (Lucas-Lehmer)   $M_p=2^p-1$ er kun et primtal hvis det går op i $S_{p-1}$:

$$S_{p-1} \equiv 0 \pmod{M_p}$$ (4.1)

hvor serien $S$ defineres således:

$$\begin{split}S_1 & = 4 S_n & = S_{n-1}^2 - 2 \end{split}$$ (4.2)

Vi starter med at indføre to symboler $\omega = 2 + \sqrt{3}$ og $\overline{\omega} = 2 - \sqrt{3}$. Vi ser at $\omega\overline{\omega} = 1$.

Der gælder nu følgende om serien $S$, $\omega$ og $\overline{\omega}$:

SÆTNING 4.2   Det $m$-te element i serien $S$ er givet ved

$$S_m = \omega^{2^{m-1}} + \overline{\omega}^{2^{m-1}}.$$ (4.3)

Vi bruger et induktionsbevis, som i [9, s. 273-275]. Der skal altså gælde to ting om (4.3):

1. $S_1$ skal være sand,
2. Hvis $S_m$ er sand, skal $S_{m+1}$ også være det. Vi kender $S_{m+1}$ fra (4.2).

Ifølge (4.2) er $S_1 = 4$. Vi ser at $\omega^{2^{1-1}} + \overline{\omega}^{2^{1-1}}$ også er lig $4$.

Vi viser så, at hvis (4.3) er sand for $m$, så er den også sand for $m+1$. $S_{m+1}$ skal så være lig $\omega^{2^n} + \overline{\omega}^{2^n}$:

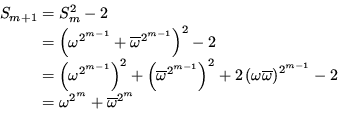$$\begin{split}S_{m+1} & = S_m^2 - 2 & = \left(\omega^{2^{m... ... - 2 & = \omega^{2^m} + \overline{\omega}^{2^m} \end{split}$$ (4.4)

Vi har nu vist at (4.3) gælder for både $m = 1$ og for $m = m + 1$, derfor gælder den for alle $m \in \mathbb{Z}$. $\blacksquare$

Vi går nu ud fra at $M_p$ går op i $S_{p-1}$, og ud fra sætning 4.2 får vi at det må betyde følgende:

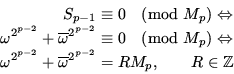$$\begin{split}S_{p-1} & \equiv 0 \pmod{M_p} \Leftrightarrow \\... ...{\omega}^{2^{p-2}} & = RM_p, \qquad R \in \mathbb{Z}\end{split}$$ (4.5)

I sidste linie skrev vi kongruensen som en normal ligning. Denne arbejder vi videre på, først ganger vi igennem med $\omega^{2^{p-2}}$ og vi flytter 1 over på højresiden:

$$\omega^{2^{p-1}} = RM_p \omega^{2^{p-2}} - 1$$ (4.6)

Vi kvadrerer:

$$\omega^{2^p} = \left(RM_p \omega^{2^{p-2}}-1\right)^2$$ (4.7)

Vi får brug for (4.6) og (4.7) lidt senere.

Vi vil gå ud fra at $M_p$ ikke er et primtal, og vil vise at dette medfører en modstrid. Hvis $M_p$ ikke er et primtal, vil der være en primfakter $q$ som opfylder at $q^2 \le M_p$.

Vi lader nu $\mathbb{Z}_q$ betegne mængden af heltal modulus $q$ og $X$ betegne mængden $\{a_1+a_2\sqrt{3}:a_1,a_2 \in \mathbb{Z}_q\}$. Vi definerer to kompositioner på mængden $X$, addition og multiplikation. I begge tilfælde reducerer vi koefficienterne med modulus $q$.

Addition defineres på normal vis:

$$(a_1+a_2\sqrt{3})+(b_1+b_2\sqrt{3}) = (a_1+b_1)+(a_2+b_2)\sqrt{3}$$ (4.8)

På samme måde defineres multiplikation som:

$$(a_1+a_2\sqrt{3})\times(b_1+b_2\sqrt{3}) = (a_1b_1 + 3a_2b_2) + (a_1b_2+b_1a_2)\sqrt{3}$$ (4.9)

Vi ser at $(X,+,\times)$ er en algebraisk struktur, da kompositionerne opfylder kravet om at de afbilder mængden $X$ ind i $X$.

Det neutrale element i $X$ med hensyn til multiplikation er $1+0\sqrt{3}$. Da der ifølge sætning C.6 højst findes ét neutralt element, er det nok at gøre prøve med $1+0\sqrt{3}$ for at vise at det virkeligt er det neutrale element:

$$(a_1+a_2\sqrt{3})\times (1+0\sqrt{3}) = (1a_1 + 0a_2)+(0a_1 + 1a_2)\sqrt{3} = a_1+a_2\sqrt{3}$$ (4.10)

Vi lader $X^*$ betegne gruppen af invertible elementer i $X$. Ved at bruge sætning 3.12 ser vi at $X^*$ er en gruppe.

Vi ser nu på $\omega = 2 + \sqrt{3}$ som et element i $X$. $\omega$ er også et element i $X^*$ da det er invertibelt: $\omega\overline{\omega} = 1$. Hvis man tænker nærmere over det, vil det først se ud som om at $\overline{\omega} = 2 - \sqrt{3}$ ikke er et element i $X$. Alle elementerne i $X$ har jo formen $a+b\sqrt{3}$ hvor $a, b \in \mathbb{Z}_q = \{0, 1, \dots q-1\}$. Koefficienterne skulle altså ikke være negative.

Men da koefficienterne bliver reduceret modulus $q$, kan de i virkeligheden have denne form:

$$X = \{(a+nq)+(b+nq)\sqrt{3}: a, b \in \mathbb{Z}_q, n \in \mathbb{Z}\}$$ (4.11)

I tilfældet med $\overline{\omega} = 2 - \sqrt{3}$, kan vi også skrive $\overline{\omega}$ som $2+(q-1)\sqrt{3}$ da $q-1$ også er kongruent med $-1$ modulus $q$. Derfor er det faktisk i orden når de i beviserne skriver $\overline{\omega} = 2 - \sqrt{3}$.

Vi valgte $q$ så det gik op i $M_p$. Derfor gælder der at

$$RM_p \omega^{2^{p-2}} \equiv 0 \pmod{q}$$ (4.12)

Set som et element i $X$ er $RM_p \omega^{2^{p-2}}$ altså lig 0, da koefficienterne reduceres modulus $q$. Ud fra det kan vi omskrive ligningerne (4.6) og (4.7) til:

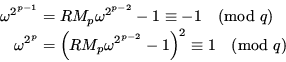$$\begin{split}\omega^{2^{p-1}} & = RM_p \omega^{2^{p-2}} - 1 \... ...(RM_p \omega^{2^{p-2}}-1\right)^2 \equiv 1 \pmod{q} \end{split}$$ (4.13)

Set som et element i $X$ får vi altså at

$$\omega^{2^{p-1}} = -1 \qquad \omega^{2^p} = 1$$ (4.14)

Da $\omega^{2^p} = 1 = e$ har vi ifølge sætning 3.11 at $\operatorname{ord}\omega$ går op i $2^p$. Vi har altså at $\operatorname{ord}\omega = 2^k$ hvor $k\le p$. Hvis vi kvadrerer $\omega^{2^k} = 1$ får vi $\omega^{2^{k+1}} = 1^2$. Bliver vi ved med at kvadrere får vi til sidst at $\omega^{2^{p-1}} = 1$, hvilket er falsk i følge (4.14). Derfor kan $k$ ikke være mindre end $p$, hvilket giver os at $\operatorname{ord}\omega = 2^p$.

Da $X^*$ består af alle de invertible elementer fra $X$, får vi at $\operatorname{ord}X^* \le q^2-1$. Der er nemlig $q$ elementer i $\mathbb{Z}_q$, og vi bruger 2 elementer til hvert element i $X$. Det giver os at der er $q^2$ elementer i $X$. Men da elementet $0+0\sqrt{3}$ ikke er invertibelt, findes der højst $q^2-1$ elementer i $X^*$.

$\omega$ er et element i $X$, da $\omega\overline{\omega} = 1$. Her er det at $\overline{\omega}=2+(q-1)\sqrt{3}$, så der gælder at både $2$ og $q-1$ er elementer i $\mathbb{Z}_q$. Vi får så ifølge sætning 3.10 at

$$\begin{split}\operatorname{ord}\omega & \le \operatorname{ord}X^* \Leftrightarrow 2^p & \le q^2-1 \end{split}$$ (4.15)

Vi har samtidig valgt $q$ sådan at $q^2 \le M_p$, hvilket giver os at

$$q^2-1 \le M_p-1 \Leftrightarrow q^2-1 \le 2^p-2$$ (4.16)

Sætter vi nu (4.15) sammen med (4.16) får vi følgende modstrid:

$$2^p \le q^2-1 \le 2^p-2$$ (4.17)

Vi har nu vist at $q$ ikke kan være en primfaktor i $M_p$. Da vi netop valgte $q$, så det ville være primfaktor, må det betyde at $M_p$ ikke har nogen primfaktorer overhoved -- $M_p$ må derfor være et primtal. $\blacksquare$

• Næste: 5. Lucas-Lehmer sætningen i
• Op: 4. Lucas-Lehmer sætningen
• Foregående: 4. Lucas-Lehmer sætningen