Næste: 3.2 Grupper Op: 3. Grupper Foregående: 3. Grupper

3.1 Algebraisk struktur

Vi starter med at se på en komposition[13, s. 133]:

DEFINITION 3.1   En komposition $*$ i en mængde $M$ er en forskrift, som knytter et hvert ordnet par af elementer fra $M$ til et element i $M$. $*$ definerer en afbildning af $M$ ind i $M$.

Man skal lægge mærke til at symbolet $*$ ikke er brugt som et gangetegn. $*$ angiver blot en vilkårlig forskrift, som f.eks. kunne være givet ved

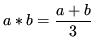$$a*b = \frac{a+b}{3}$$ (3.1)

Ud fra en komposition får vi så en algebraisk struktur:

DEFINITION 3.2   En algebraisk struktur er en mængde, $M$, hvortil der er knyttet en komposition, $*$. Dette skrives som $(M,*)$.

Vi kan nu se, at vi allerede kender mange algebraiske strukturer. F.eks. har vi at $(\mathbb{Z},+)$ er en algebraisk struktur, da der gælder

$$\forall a,b\in \mathbb{Z}:\quad a+b \in \mathbb{Z}$$ (3.2)

Næste skridt ville så være at fastlægge, hvordan vi ville regne med elementerne i en algebraisk struktur. Men da disse regler blot er udtryk for en mere formel beskrivelse af de regler vi allerede kender, er de flyttet til bilaget, se afsnit C.1. Vi vil dog lige ridse definitionerne op:

For at den associative lov er opfyldt for kompositionen $*$, skal der gælde følgende

DEFINITION 3.3   En komposition $*$ i en mængde $M$ er associativ, hvis den opfylder

$$\forall a,b,c\in M:\quad (a*b)*c = a*(b*c)$$ (3.3)

En algebraisk struktur med en associativ kompositon $(M,*)$ kaldes en semigruppe.

Vi har også den kommutative lov:

DEFINITION 3.4   En komposition $*$ i en mængde $M$ er kommutativ hvis den opfylder at

$$\forall a, b\in M:\quad a*b=b*a$$ (3.4)

Er $(M,*)$ er semigruppe, og er $*$ kommutativ, har vi en kommutativ semigruppe.

I nogle algebraiske strukturer findes et element som er neutralt.

DEFINITION 3.5   I en algebraisk struktur $(M,*)$ er elementet $e$ neutralt hvis der gælder at

$$\forall a \in M:\quad a*e = e*a = a$$ (3.5)

Ved addition kaldes det neutrale element for et nul-element mens det kaldes et et-element ved multiplikation.

Når vi så har en vilkårlig semigruppe med et neutralt element, kan vi definere et omvendt element:

DEFINITION 3.6   Når $a$ er element i semigruppen $(M,*)$ med det neutrale element $e$, og ligningssystemet

$$x*a=e,\qquad a*x=e$$ (3.6)

har en løsning, er $a$ invertibelt. Løsningen kaldes det inverse element til $a$ og betegnes med $a^{-1*}$.

• Næste: 3.2 Grupper
• Op: 3. Grupper
• Foregående: 3. Grupper