


Næste: 2.2 Restklasser
Op: 2. Kongruens og modulusregning
Foregående: 2. Kongruens og modulusregning
Vi starter med at definere kongruens:
D
EFINITION 2.1
Hvis differencen mellem to tal
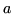
og
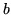
er delelig af et andet tal
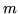
, siger vi at
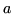
er kongruent med
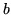
modulus
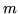
, og det skrives
således:
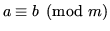 |
(2.1) |
Vi kan også skrive det som en almindelig ligning i stedet:
 |
(2.2) |
Det var C. F. Gauss (1777-1855) som opfandt denne notation[11, s.
69]. Notationen ligner den vi bruger til almindelige
ligninger, og det viser sig at man kan regne på kongruenserne efter
nogle specielle regler. Det var et stort fremskridt, da man nu havde
fået et værktøj til at beskrive de ting, der sker når tal går op i
hinanden.
Da de fleste af de følgende sætninger er ret trivielle at bevise,
har jeg flyttet beviserne over i bilaget, se
side ![[*]](../../../../images/latex-icons/crossref.png) .
.
SÆTNING 2.3
Vi kan gange både
og
med det samme tal:
. Som et specialtilfælde har vi
at
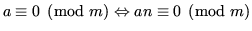
.
SÆTNING 2.4
Kongruenser modulus det samme tal kan lægges sammen og trækkes fra
hinanden: Hvis
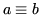
og
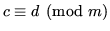
så gælder der at
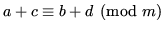
.
SÆTNING 2.5
Kongruenser modulus det samme tal kan også ganges sammen: Hvis
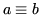
og
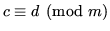
så gælder der at
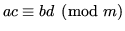
. Hvis vi gentager processen får vi at der også gælder at:
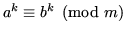
.
SÆTNING 2.7
Vi kan lægge et helt antal
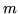
til eller trække det fra
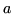
, og vil
stadig få samme rest:
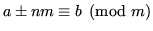
.
SÆTNING 2.8
Kongruensen
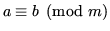
er kun
sandt, hvis der samtidig gælder at
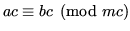
.
SÆTNING 2.9
Hvis
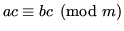
og største
fælles divisor for
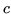
og
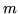
er
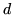
, så gælder der at
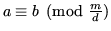
. Hvis
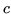
og
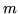
er indbyrdes primiske (
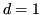
), og
vi får så at
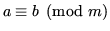
.
-
-
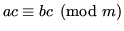 kan skrives om til
kan skrives om til
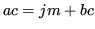 . Den største
fælles divisor for
. Den største
fælles divisor for 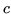 og
og 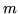 er
er 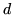 , så der gælder så også at
, så der gælder så også at
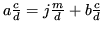 . Her er alle brøkerne
heltal, da
. Her er alle brøkerne
heltal, da 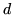 går op i både
går op i både 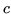 og
og 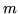 .
.
Vi kan så gange igennem med
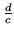 , og får så at
, og får så at
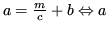 hvilket viser at
hvilket viser at 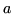 er kongruent
med
er kongruent
med 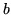 modulus
modulus
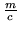 .
.

Som et eksempel kan vi se på kongruensen
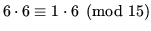 . Her har vi at største fælles divisor for 6 og 15 lig 3. Vi
kan derfor omskrive kongruensen til
. Her har vi at største fælles divisor for 6 og 15 lig 3. Vi
kan derfor omskrive kongruensen til
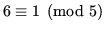 , hvilket
tydeligvis også er sandt.
, hvilket
tydeligvis også er sandt.


 Copyright © 2001, Martin Geisler.
Copyright © 2001, Martin Geisler.
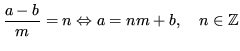
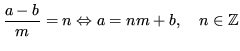
![]() .
.
![]() , og får så at
, og får så at
![]() hvilket viser at
hvilket viser at ![]() er kongruent
med
er kongruent
med ![]() modulus
modulus
![]() .
.
![]()
![]() . Her har vi at største fælles divisor for 6 og 15 lig 3. Vi
kan derfor omskrive kongruensen til
. Her har vi at største fælles divisor for 6 og 15 lig 3. Vi
kan derfor omskrive kongruensen til
![]() , hvilket
tydeligvis også er sandt.
, hvilket
tydeligvis også er sandt.