


Næste: 2. Kongruens og modulusregning
Op: 1.3 Mersenne primtal
Foregående: 1.3.2 Sætninger om Mersenne
Som med det meste talteori, har Mersenne primtal ikke nogen særlig
konkret betydning. Men man må dog nævne at Mersenne primtallene er
knyttet sammen med de perfekte tal. Om et perfekt tal gælder
D
EFINITION 1.8
Et tal
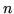
er perfekt, hvis det er lig summen af dets (positive)
divisorer, undtagen tallet selv. Derfor er 6 et perfekt tal, da
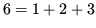
. Det samme er 28, da
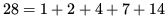
.
Perfekte tal er rimelig sjældne. Man kender også kun lige
perfekte tal, men har endnu ikke kunne give noget bevis hverken for
eller imod, at der skulle findes et ulige perfekt tal. Men man ved at
et eventuelt ulige perfekt tal må være stort[11, s. 167], da
man ved hjælp af computere har undersøgt alle tal op til 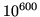 !
!
Hvert Mersenne primtal vi finder, giver os samtidig et lige perfekt
tal[14, s. 81] ifølge sætning 1.9:
SÆTNING 1.9
For hvert Mersenne primtal
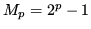
gælder der at
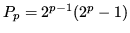
er et lige perfekt tal.
Før vi kan bevise sætning 1.9 må vi først
introducere funktionen 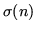 , se [7]:
, se [7]:
DEFINITION 1.10
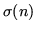
betegner summen af de positive divisorer til
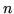
. Vi har
så for et primtal
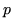
at
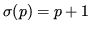
og at
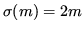
hvis
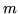
er et perfekt tal.
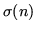
har den egenskab at
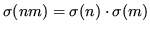
når
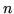
og
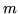
er indbyrdes primiske.
Der er lige en lille sætning vi også skal bruge, beviset for sætningen
har jeg selv lavet:
-
- Hvis vi opløser
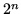 i dets primfaktorer, får vi naturligvis
i dets primfaktorer, får vi naturligvis 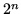 .
Derfor kan f.eks. 3 eller 5 ikke gå op i
.
Derfor kan f.eks. 3 eller 5 ikke gå op i 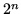 . En divisor skal så
selv have formen
. En divisor skal så
selv have formen 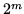 hvor
hvor 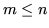 . Der må altså være
. Der må altså være 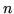 af disse
divisorer, da
af disse
divisorer, da 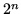 er delelig med et hvert tal på formen
er delelig med et hvert tal på formen 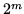 :
:
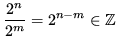 |
(1.12) |
Divisorerne er altså
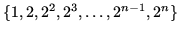 . Deres
sum er:
. Deres
sum er:
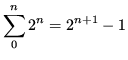 |
(1.13) |
Derved har vi vist at summen af divisorerne,
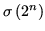 ,
er lig
,
er lig 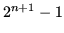 .
.

Vi kan så bevise sætning 1.9 som i
[3]:
-
- Vi går ud fra at
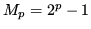 er et primtal, og skal vise at
er et primtal, og skal vise at
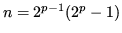 er et (lige) perfekt tal, hvilket er det samme som
at
er et (lige) perfekt tal, hvilket er det samme som
at
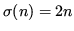 .
.
Vi har altså:
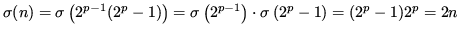 |
(1.14) |
Vi benyttede undervejs at 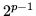 og
og 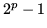 er indbyrdes primiske,
da
er indbyrdes primiske,
da 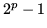 er et primtal som i hvert tilfælde ikke går op i
er et primtal som i hvert tilfælde ikke går op i
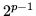 . Det viser at
. Det viser at 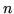 er et perfekt tal og at det må have formen
er et perfekt tal og at det må have formen
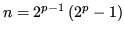 .
.
Vi kan også vise at det omvendte gælder, nemlig at hvis 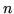 er et lige
perfekt tal, så vil det kunne skrives som
er et lige
perfekt tal, så vil det kunne skrives som
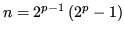 .
.
Vi har altså et lige perfekt tal, 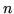 . Det må vi kunne skrive som
. Det må vi kunne skrive som
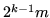 hvor
hvor 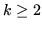 og
og 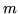 er et ulige heltal. Vi regner nu på
er et ulige heltal. Vi regner nu på
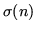 :
:
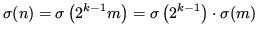 |
(1.15) |
Det giver os at
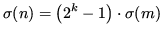 |
(1.16) |
Vi benyttede at 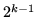 og
og 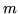 må være indbyrdes primiske, da
må være indbyrdes primiske, da
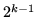 kun har primtalsdivisoren 2 og
kun har primtalsdivisoren 2 og 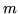 er ulige og derfor ikke
delelig med 2.
er ulige og derfor ikke
delelig med 2.
Vi ved også at 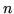 er et perfekt tal:
er et perfekt tal:
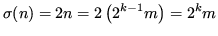 |
(1.17) |
Kombinerer vi de to sidste ligninger får vi
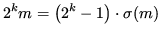 |
(1.18) |
hvilket betyder at 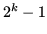 går op i
går op i 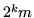 . Men
. Men 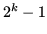 kan ikke gå op
i
kan ikke gå op
i 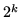 , og må derfor gå op i
, og må derfor gå op i 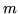 . Vi kan altså skrive
. Vi kan altså skrive 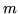 som
som
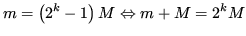 |
(1.19) |
hvor
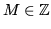 . Sætter vi
. Sætter vi
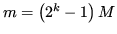 ind i
(1.18), får vi:
ind i
(1.18), får vi:
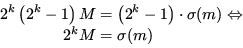 |
(1.20) |
Både 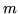 og
og 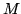 er divisorer i
er divisorer i 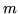 . Da
. Da 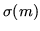 netop er summen af
divisorerne i
netop er summen af
divisorerne i 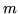 (som der godt kan være flere af ud over
(som der godt kan være flere af ud over 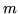 og
og 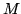 ),
må
),
må 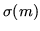 være større end eller lig
være større end eller lig 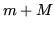 . Men da
. Men da 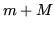 samtidig er lig
samtidig er lig
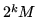 ifølge (1.19), har vi at
ifølge (1.19), har vi at
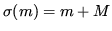 |
(1.21) |
Det viser at der kun kan være to divisorer i 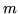 . Hvis nu
. Hvis nu 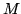 var lig
var lig
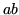 , skulle vi have fået
, skulle vi have fået
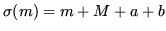 .
. 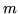 må så være et
primtal, og
må så være et
primtal, og 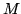 må være lig 1.
må være lig 1.
Vi har altså at 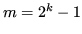 er et primtal. Tallet
er et primtal. Tallet 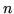 får så formen
får så formen
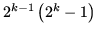 , hvilket var det vi skulle vise.
, hvilket var det vi skulle vise.

Som et eksempel på brugen af sætning 1.9, kan vi se
at tallet
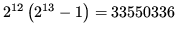 er et perfekt tal, da
er et perfekt tal, da
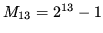 er et primtal.
er et primtal.


 Copyright © 2001, Martin Geisler.
Copyright © 2001, Martin Geisler.
![]() !
!
![]() , se [7]:
, se [7]:
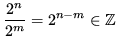
![]() . Deres
sum er:
. Deres
sum er:
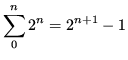
![]() er et lige
perfekt tal, så vil det kunne skrives som
er et lige
perfekt tal, så vil det kunne skrives som
![]() .
.
![]() . Det må vi kunne skrive som
. Det må vi kunne skrive som
![]() hvor
hvor ![]() og
og ![]() er et ulige heltal. Vi regner nu på
er et ulige heltal. Vi regner nu på
![]() :
:
![]() er et perfekt tal:
er et perfekt tal:
![]() er et primtal. Tallet
er et primtal. Tallet ![]() får så formen
får så formen
![]() , hvilket var det vi skulle vise.
, hvilket var det vi skulle vise.
![]()
![]() er et perfekt tal, da
er et perfekt tal, da
![]() er et primtal.
er et primtal.